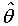 で表す。(ただし、講義ノート中では、θhatと表記する。)
例えば、θを母平均とすると、それを推定するための標本平均は推定量と見なせて、
で表す。(ただし、講義ノート中では、θhatと表記する。)
例えば、θを母平均とすると、それを推定するための標本平均は推定量と見なせて、
- θhat = (X1 + ... + Xn) / n
となる。一般に推定量θhatはX1, X2, ..., Xnの関数の形で表される。
- P(L <= θ <= U) >= 1-α
となるようなL、Uを求めることになる。ここで、L、UはX1, X2, ..., Xnの関数になっており、統計量である。区間推定も、推定量θhatの標本分布から計算される。
担当: 菊地
である。ただし、Xiはそれぞれ独立でN(μ,σ2)に従うものとする。
この時、Xmeanの標本分布は、N(μ,σ2/n)である。正規分布表を用いて、確率を計算するためには、N(0,1)に標準化しなければならないが、σ2がわかっているので標準化が可能である。(標準化した確率変数をZとする。)
また、Xmeanの標準偏差(標準誤差)はσ/√nであり、このことから次のことが言える。
鉛筆の長さの測定の例で考える。
によって計算される。この標本分散は、正規母集団を仮定しなくても、E(s2)=σ2であるが、さらに正規母集団を仮定すると、その期待値だけでなく、標本分布を求めることができる。標本分布を考えることで、母分散についての統計的推測を行うことができる。
とし、このχ2の従う確率分布を自由度kのχ2(カイ二乗)分布と呼ぶ。なお、χ2(k)で表す。また、χ2(k)の上側確率がαとなる値をχα2(k)と書き、χ2分布表として掲載されている。
ここで、標本分散について考える。正規母集団からの標本による標本分散s2から得られる統計量
は、自由度n-1のχ2分布χ2(n-1)に従うことが知られている。
s2=50として、χ2値を計算すると、χ2=(n-1)s2/σ2=9*50/25=18である。χ2分布表から、自由度9のχ2分布の上側確率を求めると、P(χ2>18)=0.038である。
すなわち、真の分散が25であっても、2倍の50を超える標本分散が出ることも、まれにはあるということであり、標本分散の大きさの解釈には注意が必要である。
標本平均Xmeanの標本分布を標準化する際のσ2の代わりに、s2を使ったスチューデントのt統計量を
と定義する。これは、N(0,1)には従わないが、式を変形するとN(0,1)とχ2(n-1)の組み合わせで書けることがわかる。
このようなt統計量が従う確率分布を(スチューデントの)t分布と呼ぶ。自由度は、含まれるχ2分布の自由度と同じであり、(Xmean-μ)/√(s2/n)は、自由度n-1のt分布に従う。なお、自由度kのt分布をt(k)と書く。t統計量の分母は、Xmeanの標準偏差s/√nであり、標本平均の標準誤差である。
t分布は正規分布の代用品であるが、大標本(n→∞)の場合には、正規分布と一致する。t(k)の上側確率100α%のパーセント点をtα(k)と書き、t分布表として教科書に掲載されている。
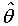 で表す。(ただし、講義ノート中では、θhatと表記する。)
例えば、θを母平均とすると、それを推定するための標本平均は推定量と見なせて、
で表す。(ただし、講義ノート中では、θhatと表記する。)
例えば、θを母平均とすると、それを推定するための標本平均は推定量と見なせて、
となる。一般に推定量θhatはX1, X2, ..., Xnの関数の形で表される。
となるようなL、Uを求めることになる。ここで、L、UはX1, X2, ..., Xnの関数になっており、統計量である。区間推定も、推定量θhatの標本分布から計算される。