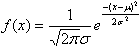数理統計II

担当: 菊地

第5回 確率分布

5.1 離散型の確率分布

二項分布とベルヌーイ分布

2種類の可能な結果(成功S、失敗Fとしておく)を生じる実験あるいは観測があり、それらの確率をそれぞれp、1-pとする。これを同じ条件で独立にn回繰り返すことをベルヌーイ試行と呼ぶ。

n回の試行のうち、Sがx回、Fがn-x回生じた時、その確率は、

f(x) = _nC_x p^x (1-p)^n-x, x=0, 1, ..., n

となる。この確率分布を二項分布と呼び、Bi(n,p)で表す。特に、試行回数n=1の場合であるBi(1,p)をベルヌーイ分布という。確率変数Xが二項分布Bi(n,p)に従う時、期待値、分散は、

E(X) = n p
V(X) = n p (1-p)

となる。これは、成功の確率がpで、n回試行した場合に、平均的にn p回成功することを表し、直感的にわかりやすい。分散の方は、p=1/2の時に最大となるが、これは成功と失敗が半々の確率で起こる時に、どちらが起こるのかが最も予想しづらいということを表している。

期待値、分散の証明はいくつかあるが、以下のものが簡単である。まず、Bi(1,p)の場合の期待値、分散を計算すると、定義から、

E(X) = 0*(1-p) + 1*p = p
V(X) = (0 - p)²*(1-p) + (1-p)²*p = p (1-p)

である。Bi(n,p)は、独立なBi(1,p)のn個の和であるから、

E(X) = n p
V(X) = n p (1-p)

となる。(分散の証明には、後に説明がある独立な確率変数の分散の加法性を用いている。)

ポアソン分布

確率変数Xが二項分布に従い、nが非常に大きく、pが非常に小さい場合を考える。例えば、n=1000、p=0.002の場合を考えると、それぞれの値の生起確率は非常に小さくなるが、E(X)=2であるので、小さい値の生起確率は小さくはないはずである。

このような場合には、ポアソンの少数の法則が利用できる。np→λという条件を保ちながら、n→∞、p→0となる極限では、

_nC_x p^x (1-p)^n-x → e^-λ λ^x / x!

が成り立つ。

すなわち、2種類の可能な結果を表す確率変数Xにおいて、nが極端に大きく、pが極端に小さい場合には、このポアソンの少数の法則を利用して確率を定義したポアソン分布に従うといえる。ポアソン分布Po(λ)は、

f(x) = e^-λ λ^x / x!

であり、

E(X)=λ, V(X)=λ

である。このようにポアソン分布では、期待値と分散が等しくなることが特徴である。これは、二項分布Bi(n,p)の期待値np、分散np(1-p)に対し、np≒λ、(1-p)≒1とした結果と一致している。

ポアソン分布は、交通事故件数や大量生産の不良品数、遺伝子の突然変異数など、リスクや安全性に関する現象に適用されることが多い。

離散一様分布

理想的なN個の目がでるさいころをふった時に出る目を確率変数Xとすると、その確率は、

f(x)=1/N

である。ただし、x=1, 2, ..., Nである。このような分布を離散一様分布と呼ぶ。その期待値、分散は、

E(X)=(N+1)/2, V(X)=(N²-1)/12

となる。

5.2 連続型の確率分布

正規分布

正規分布は、代表的な確率分布であり、多くの現象にあてはまり、また統計学の理論上も応用上も非常に重要である。正規分布の密度関数は、

で定義され、ガウス分布とも呼ばれる。平均μ、分散σ²に従う正規分布を、N(μ,σ²)で表す。

測定誤差は、正規分布に従うとされるので、測定を行う場合には正規分布が関係してくる。また、生物測定の分野ではあてはまる場合が多い。

正規分布の特徴は以下のようなものである。

a) XがN(μ,σ²)に従っている時、その線形変換Y=aX+bはN(aμ+b,a²σ²)に従う。
b) 標準化変数Z=(X-μ)/σは正規分布N(0,1)に従う。これを標準正規分布と呼ぶ。

このことから、いかなる正規分布の確率計算も、標準正規分布を用いたものに帰着できる。

標準正規分布の累積分布関数は、正規分布表として多くの教科書にのっているが、主な区間の確率がよく知られている。

P(-1 <= Z <= 1) = 0.6827 (ほぼ2/3)
P(-2 <= Z <= 2) = 0.9545 (ほぼ95%)
P(-3 <= Z <= 3) = 0.9973 (ほぼ100%)

なお、-3<=Z<=3は、もとのXでいえば-3σ<=X<=3σに相当し、常識的に考えるとすべての観測値がこの範囲に入る。このことから、「事実上のすべて」という意味で3シグマ範囲と呼ばれることがある。

入試などで用いられる偏差値は、得点を平均が50、標準偏差が10(分散が100)になるように標準化したものである。得点分布が正規分布に従うとすると、偏差値が40〜60の範囲(平均±1×標準偏差)に2/3の受験者が入り、30〜70の範囲(平均±2×標準偏差)に95%の受験者が入ることになる。

また、同一の確率分布f(x)を持つn個の独立な確率変数の和X₁+X₂+...+X_nは、nが大きくなると、もとの分布が何であろうと正規分布に近付く。データから計算された算術平均(標本平均)は、同一の確率変数の和をnで割ったものなので、正規分布をすると見なせる。これは中心極限定理によって示されている。

そして、正規分布には、再生性という有用な性質がある。独立な確率変数X, Yが正規分布N(μ_X, σ_X²), N(μ_Y, σ_Y²)に従うとき、aX + bYは正規分布N(a μ_X + b μ_Y, a² σ_X² + b² σ_Y²)に従う。

対数正規分布

Xの対数をとったlog Xが正規分布に従うならば、もとのXの分布を、対数正規分布と呼ぶ。小さい値には限度があるが、大きい値の方に限度がないような、対数をとった方が良いと思われるデータに用いられる。例えば、各世帯の年間所得のデータなどがある。

5.3 共分散と相関係数

V(X+Y) = E((X - E(X)) + (Y - E(Y)))²
= V(X) + 2 E((X - E(X)) (Y - E(Y))) + V(Y)

となる。すなわち、一般的に、V(X+Y) ≠ V(X) + V(Y)である。これは、XとYが互いに関連しながらばらつく要素である共分散が存在するためである。この共分散をCov(X,Y)と書き、

Cov(X,Y) = E((X - E(X)) (Y - E(Y)))
= E(XY) - E(X) E(Y)

と定義する。共分散は、正の相関があれば正、負の相関があれば負となる。また、2つの確率変数X, Yの相関係数ρ_XYは、

ρ_XY = Cov(X,Y) / (√V(X) √V(Y))

として定義される。ρ=0の場合、XとYは関連しないことを表し、無相関であるという。なお、XとYが独立であれば無相関であるが、無相関であっても独立とはいえない。独立な場合には、以下の性質が成り立つ。

E(XY) = E(X) E(Y)
Cov(X,Y) = E(XY) - E(X) E(Y) = 0
ρ_XY = 0

5.4 独立な確率変数の和

分散の加法性

2つの確率変数が独立なとき、分散に対して加法性が成り立つ。

V(X±Y) = V(X) + V(Y)

なお、この加法性については、無相関の条件で十分である。また、期待値に対しては、加法性E(X+Y)=E(X)+E(Y)が常に成り立つ。

n個の確率変数X₁, X₂, ..., X_nに対しても、独立の時には、

V(X₁+X₂+...+X_n)=V(X₁)+V(X₂)+...V(X_n)

が成り立つ。

独立同一分布

確率変数X₁, X₂, ..., X_nが独立で同一の分布に従うとし、これらの期待値、分散をμ、σ²とすると、

E(X₁+X₂+...+X_n)=n μ
V(X₁+X₂+...+X_n)=n σ²

となる。

相加平均

確率変数X₁, X₂, ..., X_nが独立同一分布に従うとし、X₁+X₂+...+X_nをnで割った相加平均を

X_mean = (X₁+X₂+...+X_n)/n

とおくと、

E(X_mean) = μ
V(X_mean) = σ²/n

となる。すなわち、相加平均X_meanの期待値は、常にμに一致するが、分散は、nに反比例し、nが大きくなるにつれ小さくなり、0に収束する。これを定理にしたものが大数の法則である。