数理統計II

担当: 菊地

第7回 標本分布と統計量

2007.6.7

7.1 標本分布

標本平均
標本X1, X2, ..., Xnから計算される算術平均。標本X1, X2, ..., Xnは、母集団分布(母平均μ)に従う独立な確率変数であり、標本平均Xmeanは、

Xmean = (X1 + X2 + ... + Xn) / n

で与えられる。ここで、Xmeanの期待値は、

E(Xmean) = E((X1 + X2 + ... + Xn) / n) = n μ / n = μ

となり、母平均μに一致する。すなわち、大きすぎ、あるいは小さすぎなどの傾向がなく、平均的に正しく推定できる統計量である。さらに、nが大きくなれば、μに集中する傾向がある。これは、Xmeanの分散は、

V(Xmean) = V((X1 + X2 + ... + Xn) / n) = V(X1 + X2 + ... + Xn) / n2 = n σ2 / n2 = σ2 / n

であり、n→∞のとき0に近付く。すなわち、Xmean→μのように確率収束するからである。

また、標本平均の分散の平方根(標準偏差)を特別に標準誤差と呼ぶことが多い。

視聴率調査の誤差
(株)ビデオリサーチの視聴率調査は、関東地区・関西地区で600世帯、名古屋地区で 250世帯、それ以外の地区は200世帯で行っている。そこで、関東地区600世帯で調査された視聴率の標本分布を考えてみる。

母集団は、関東地区の全世帯である。ある世帯でその番組を見る、見ないという現象は、二項分布に従い、その番組を見る確率をpとしておく。すなわち、この場合の母集団分布は生起確率がpの二項分布である。

この調査で観測されるn(=600)個の確率変数Xiが、番組を見ている場合には1、見ていない場合には0を取るものとすると、発表されている視聴率は、このXiの標本平均である。また、確率変数Xiの分散は、二項分布の分散p(1-p)で表されるので、母分散σ2は、

σ2=p (1-p)
となる。

よって、この調査の標準誤差は、上の標本平均の分散V(Xmean)の平方根なので、

√(p(1-p)/n)
となる。

例えば、母視聴率が30%の番組があり、これについて600世帯で調査を行うと、その標準誤差は、0.3*0.7/600の平方根であり、1.87%である。 標準誤差の性質として、標本から計算した統計量は(真の値±1.96*標準誤差)の間に95%の確率で入ることが知られている。

標準誤差は、標本の大きさnが大きくなればなるほど、小さくなる。逆に、例えば、この調査を200世帯で行った場合には、標準誤差は3.24%と大きくなってしまう。

7.2 正規分布の重要性

標本平均、標本分散など、多くの統計量が中心極限定理により、正規分布に従ったり、正規分布から求まる分布に従う。また、いわゆる測定の際の誤差も、正規分布に従うため、重要である。

正規分布の利用法
ある標本の標本平均から、母平均(真の平均)がどれくらいか見当をつけたい。

母平均の値を仮定
(真の値の見当をつける)
↓
標本平均の値を計算
↓
仮定した母平均の値が正しいとしたときの標本平均の分布を求める
(見当をつけた値が正しいとして求める)
↓
実際に求めた標本平均の値がどれくらいの確率で起きるのか求める
↓
当たり前に起こる場合には仮定が正しく、通常は起こり得ない場合には仮定が間違っていると判断する
(見当のつけ方が正しいかどうか判断する)

なお、このときの標本平均の分布は正規分布から求まる。

7.3 測定

1本の鉛筆の長さを測るという測定(観測)を考える。

測定条件を同じにして、n回測定を行い、その測定値をX1, X2, ..., Xnとする。これを得られた標本と考えると、母集団は、鉛筆の長さの測定値全体(無限回繰り返して測定できるので無限にある)と考えられる。

各Xiは、(真の値)+(測定誤差)という形で表されるはずなので、μを真の値、eiをi回目の測定の誤差とすると、

Xi = μ + ei

と書ける。ただし、真の値は未知である。

誤差は、ランダムな値であり、すべて独立で同一の確率分布を持っていると仮定できる。ガウスの誤差理論によって、この測定誤差の分布は平均0、分散σ2の正規分布N(0,σ2)であることが、示されている。すなわち、誤差は確率変数であり、正の場合も、負の場合もあるが、平均は0である。また、精度の良い測定では、誤差分散が小さく、悪い測定では誤差分散が大きくなる。

測定値Xiは、(真の値)+(測定誤差)であるから、誤差に真の値(定数μ)を加えたものであり、N(μ,σ2)に従うことになる。すなわち、測定値そのものも、正規分布に従うということになる。

7.4 正規分布の性質

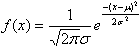正規分布N(μ,σ2)の密度関数は、で定義されており、密度関数はμに関して対称である。このため、メディアン、モードは、平均と一致する。ガウス分布とも呼ばれ、正規分布に従う確率変数を、正規確率変数、ガウス(型)確率変数と呼ぶ。

正規分布の性質
  1. 身長の分布や実験誤差の分布など、分析対象となる現象は正規分布で表せるものが多い。
  2. 体重や所得のように変数変換によって(体重は1/3乗、所得は対数変換)、正規分布で表せるものが多い。
  3. 標本平均など多くの統計量が確率変数の和の形になっていて、標本の大きさが大きくなると、正規分布に従うものが多い。
  4. 独立な正規確率変数の和は正規確率変数となるなど数学的な扱いが容易で、標本分布を近似ではなく正確に求めることができる。
    1. 正規確率変数の線形変換は正規確率変数になる。
    2. 独立な二つ以上の正規確率変数の和および差は正規確率変数になる。
標準正規分布
平均が0、分散が1の正規分布N(0,1)のことであり、累積密度関数の値が、多くの教科書で正規分布表として与えられている。

実際の場面で、正規分布表を用いるためには、一般の正規分布を標準正規分布に変換しなければならない。XがN(μ,σ2)に従えば、

Z = (X - μ) / σ

という標準化を行うことで、ZはN(0,1)に従うように変換される。